純粋型システムとλキューブ

公開日: 2022/10/08

この記事では、型システムの統一的な定式化を与える 純粋型システム と呼ばれる枠組みを紹介し、それをもとに λキューブ として8つの型システムを導入する。

非形式的な説明

抽象化の方法

型システムにおいて重要な対象は関数である。関数は入力を受け取って出力を返すものと見ることもできるが、より一般的にはプログラムの一部を変数として 抽象化(abstract) ないし パラメータ付け(parameterize) したものと見ることができる。

さて、どのようなプログラムの中で何を抽象化するかについては、複数の場合がありえる。どの抽象化の方法を許容するかによって、その型システムの表現力が様々に変わることになる。ここでは、プログラムの要素として項と型を考え、合計2×2の4通りを例とともに見る¹。

① 項の中の項を抽象化

これは通常の関数のことである。同じような処理を何度も書くことを避けるために、プログラムの一部を変数にして特定の処理を関数にするのはよくある手法である。これを「項の中の項を抽象化する」と言い直しているだけである。

以下の例は自然数に1を足す関数を表している。なお、自然数の型 Nat やその上の演算は予め定義されているものとする。

plus_one : Nat → Natplus_one n = n + 1

このような関数は plus_one = λ(n : Nat). n + 1 のようにλ記号を使って書かれることもある。

② 項の中の型を抽象化

これはいわゆる 多相関数(polymorphic function) である。型によらず同じ処理をする関数を1つにまとめるようなイメージである。例えば、以下の関数 id は任意の型の項を受け取り、それをそのまま返す恒等関数である。

id : Π(A : Type). A → Aid A x = x

Type は「型の型」のようなものであり(詳細は後述)、A は型が代入されるような変数になっている。これに型を渡すことによって、id は A の項を受け取る関数になる²。以下の例では、Aとして自然数の型 Nat を入力している。

id_nat : Nat → Natid_nat = id Natone : Natone = id_nat 1

③ 型の中の項を抽象化

これは「項に依存する型」ということで 依存(関数)型(dependent (function) type) と呼ばれ、非形式的には入力の値によって出力の型が変わるような関数の型と説明できる(依存型が入力を受け取るわけではないので注意)。より具体的には、依存型 $\Pi x{:}A.B$ に属する項 $$f$$ は、入力 $$a:A$$ に対して出力 $$f(a):B[x:=a]$$ を返す。

なお、依存型は通常の関数型の一般化であると言える。実際、依存型 $\Pi x{:}A.B$ であって $x\notin\FV(B)$ であるようなものは、関数型 $A\to B$ と見なせる。

以下に依存型の例を挙げるが、関数型プログラミングに慣れていないと分かりにくいと思われるので、読み飛ばしても構わない。浮動小数点数Floatのリスト型を拡張して、次のように「長さn(固定長)のFloatリスト型」を定義することを考える。

data FloatList : Nat → Type where    nil : FloatList 0    cons : Π(n : Nat). Float → FloatList n → FloatList (n + 1)

このとき、cons は依存型に属する項になっているため、例えば cons 2 は長さ2のリストと値を結合する関数となり、それ以外の長さの入力は受け付けない。

list : FloatList 3list = cons 2 0.125 (cons 1 0.24 (cons 0 0.375 nil))    -- list = [0.125 , 0.25 , 0.375]

このようにして、リストを入力として受け取る関数の仕様をより詳細に記述できる。例えばリストの間で内積を定義したい場合には、入力として受け取る2つのリストの長さが等しいことを依存型によって保証できる。

dot : Π(n : Nat). FloatList n → FloatList n → Floatdot = ...

補足.

なお、カリー・ハワード同型対応に基づいて命題を型と見なすならば、依存関数型は1階述語論理における全称量化に対応する。例として、自然数上の加法の可換性を表す命題

P ~\defeq~ \forall m, n\in\N. m + n = n + m

を考えると、これは依存型 Π(m n : Nat). ... として表現できる。よって、例えば $$1+2=2+1$$ という命題は「依存型 P に 1 と 2 を入力として渡して得られる型」と見なせる。さらに、「命題の証明」は「型に属する項」に対応するので、命題 $$P$$ の証明(すなわち項 f : P )に対して $$1,2$$ を入力として渡せば、 $$1+2=2+1$$ の証明が得られる(下のコードを参照)。

proof : Π(m n : Nat). m + n ≡ n + mproof = ...    -- ここに証明を書くproof_one_two : 1 + 2 ≡ 2 + 1proof_one_two = proof 1 2

このように全称量化された命題の証明を「要素を受け取って証明を返す関数」と見なす考え方は、構成主義におけるBHK解釈(BHK interpretation)に基づく。詳しくは直観主義1階述語論理の記事を参照のこと。

(閉じる)

④ 型の中の型を抽象化

これは①(通常の関数)の型バージョンであり、型構成子, 型構築子(type constructor) などと呼ばれる。例えば次の関数は2つの型を受け取り、その直積を返している。

prod : Type → Type → Typeprod A B = A × B

型とカインド

以上のように様々な種類の抽象化を考えるときに注意しなければならないのは、関数に対して適切ではない入力が渡されないようにすることである。通常の関数を扱う程度の範囲では、このことは型が項を分類することによって保証される。例えば plus_one : Nat → Nat や "abc" : String と型が付いていることにより、plus_one "abc" のような誤った組み合わせを防ぐことができる。

しかし、③や④のように型において抽象化がなされる場合、型に対しても適切な分類を与える必要がある。例えば上で登場した prod は第1引数に型 A : Type を受け取るべきであるから、prod prod のようなプログラムは排除しなければならない。

このために使われるのが カインド(kind) である。カインドは型を分類するものであり、いわば「型の型」である。カインドの例を以下にいくつか挙げる。

Type : 項を分類する型が属するカインド³⁴
- 属する対象の例: Nat, Nat → Nat, Π(A : Type). A → A⁵, Π(n : Nat). FloatList n → FloatList n → FLoat
- カインドに分類される対象を指す「型」という用語と区別するために、これらの(項を分類するものとしての)型を特に 真の型(proper type) ということがある。
Type → Type → Type : 2引数の型構成子が属するカインド
- 属する対象の例: prod
Nat → Type : 自然数を受け取って型を返す関数が属するカインド
- 属する対象の例: FloatList

型にとってのカインドは項にとっての型であり、「項 : 型 : カインド」という階層構造ができることになる。これまでに登場した例をまとめて図示すると、下図のようになる(赤い点線の矢印が所属関係を表す)。

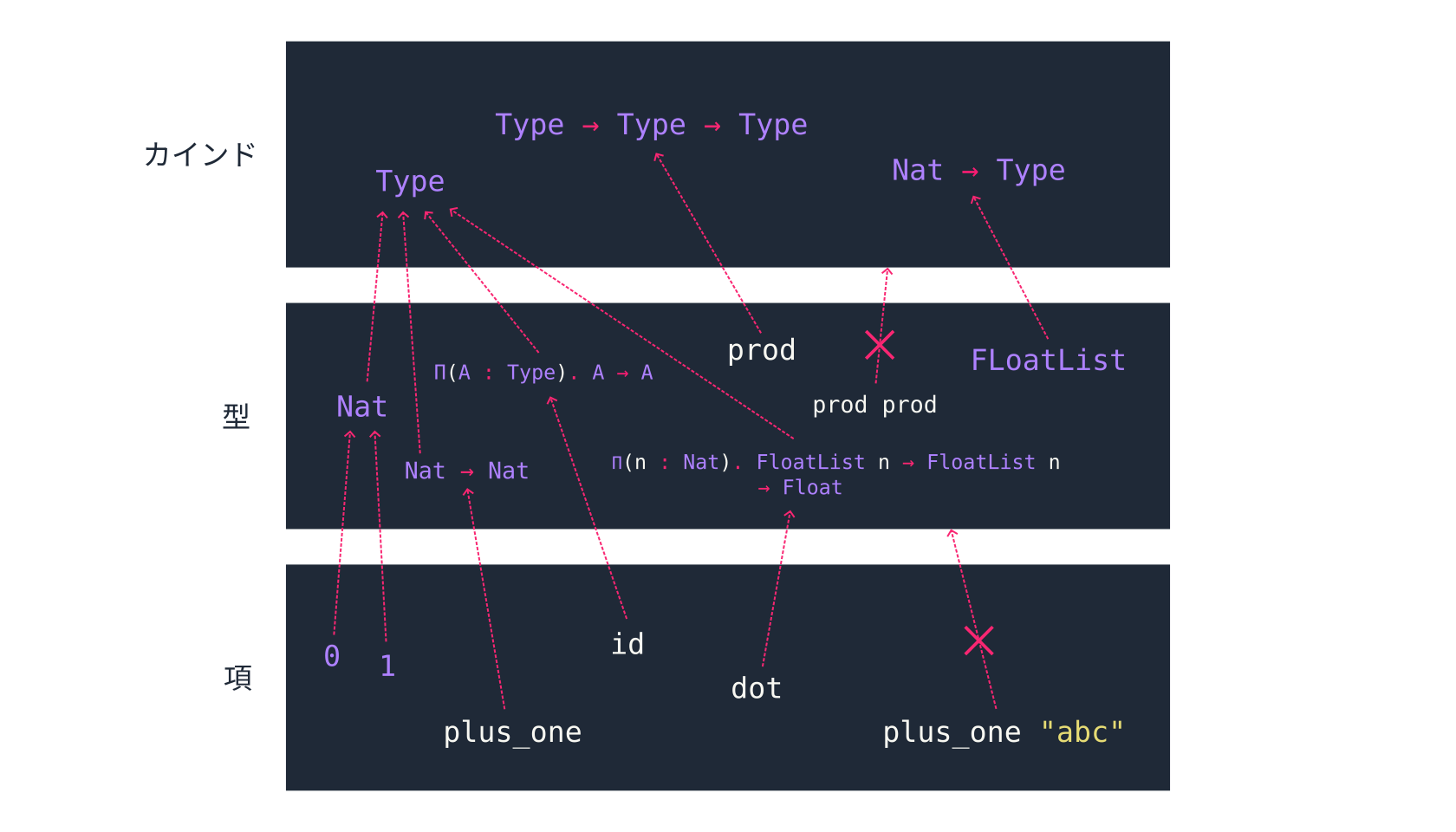
項・型・カインドがなす階層構造

以上で4種類の抽象化の方法を導入した。本記事のテーマの1つであるλキューブを理解する上ではこの4つがあれば十分だが、他にも抽象化のパターンは様々に存在する。例えば、

カインドの中でも項・型・カインドを抽象化することができる。この場合、カインドを分類するための上位のモノ(例えば、カインド全体の集まり Kind )が必要になる。
さらに上位の対象へと分類を与えていくことで、カインドの階層を Type : Type' : Type'' : ... のように重ねていくことができる(このような場合、これらは ソート(sort) や 宇宙(universe) と呼ばれる)。
Type と並列して、型を分類するような別のカインドを導入することもできる⁶。

このような様々な抽象化のあり方を記述できるのが、次に説明する純粋型システムである。

純粋型システム

以下では、加算無限個の変数の集合 $\Var$ が与えられているものとする。メタ変数として、変数を $$x,P$$ など、項や型を $$M,N,A,B$$ などで表す。

定義. 純粋型システム

純粋型システム(pure type system) を、以下から成る組 $\tuple{\sorts,\axioms,\rules}$ とする。

$\sorts$ : 非空な集合
$\axioms\sube\sorts^2$
$\rules\sube\sorts^3$

$\sorts,\axioms,\rules$ の元をそれぞれ ソート(sort), 公理(axiom), 規則(rule) という。 $\tuple{s_1,s_2,s_3}\in\rules$ に対して、 $$s_2=s_3$$ のとき $$(s_1,s_2)$$ と略記する。

ソートはカインドを一般化したものであり、公理はその間の階層関係を記述したものである。そして規則は、抽象化の方法として何を許容するかを規定する (ただし「公理」「規則」という言葉は一般名詞としても使うので注意されたい)。

次に構文に関する定義を行うが、構文的には項や型の間の区別がなされないことに注意する必要がある。項 : 型 : カインド : ... といった階層的区別は、後述の推論規則によって与えられる。

定義. 前項

純粋型システム $\tuple{\sorts,\axioms,\rules}$ の 前項(preterm) の集合 $\Lambda$ を以下のBNFで定める。補助記号の括弧は適宜省略する。

A ::= x\mid s\mid AA\mid \lambda x{:}A. A \mid \Pi x{:}A. A

自由変数 $\FV(A)$ や代入操作 $$A[x:=B]$$ は通常通り定義し、また $\alpha$ 同値な表現を同一視する。

また、 $\Pi x{:}A.B$ において $x\notin\FV(B)$ のとき、これを $A\to B$ と略記することがある。

定義. 文脈・判断

文脈(context) を以下のBNFで定める。空の文脈 $\tuple{}$ は適宜省略するものとする。

\Gamma ::= \tuple{} \mid x : A, \Gamma

文脈 $\Gamma=x_1:A_1,\ldots,x_n:A_n,\tuple{}$ に対して、その定義域(domain)を集合 $\qty{x_1,\ldots,x_n}$ とし、 $\mathrm{dom}(\Gamma)$ で表す。

また、文脈 $\Gamma$ と $M,A\in\Lambda$ に対して、 $\Gamma\vdash M:A$ を 判断(judgement) という。

定義. 簡約

前項に対する簡約の簡約基を以下により定める。

(\lambda x{:}A. B)C \mapsto B[x:=C]

これによって定まる合同関係を $\to_\beta$ で表す(1ステップの簡約)。また、この反射推移閉包を $\twoheadrightarrow_\beta$ とし(0ステップ以上の簡約)、これにより定まる同値関係を $=_\beta$ で表す。

以上を踏まえて、純粋型システムにおいて判断を導出するための規則を導入しよう。これは通常の型システムにおける型付け規則と同様のものである。

定義. 推論規則・導出可能性

純粋型システム $\tuple{\sorts,\axioms,\rules}$ の推論規則を以下のように定義する。ただし、推論規則は一般に次の形式で書くものとする(各 $J_1,\ldots,J_n$ は前提( $n\in\N$ ), $$J$$ は結論)⁷。

\begin{prooftree} \AXC{$J_1\quad\cdots\quad J_n$} \RightLabel{$~\small\text{(追加の条件)}$} \UIC{$J$} \end{prooftree}

(Ax): ソート間の階層関係を与える。

\begin{prooftree} \AXC{} \RightLabel{$~\small(\tuple{s_1,s_2}\in \axioms)$} \UIC{${}\vdash s_1:s_2$} \end{prooftree}

(Var): 変数を導入する。

\begin{prooftree} \AXC{$\Gamma\vdash A:s$} \RightLabel{$~\small(x\notin\mathrm{dom}(\Gamma))$} \UIC{$\Gamma,x:A{}\vdash x:A$} \end{prooftree}

(Prod): 各ソートに属する対象を形成する。 $\rules$ の規則によって抽象化の方法が規定されている。

\begin{prooftree} \AXC{$\Gamma\vdash A:s_1$} \AXC{$\Gamma,x:A\vdash B:s_2$} \RightLabel{$~\small (\tuple{s_1,s_2,s_3}\in\rules)$} \BIC{$\Gamma\vdash \Pi x{:}A. B:s_3$} \end{prooftree}

(Abs): Prod規則で形成された対象に属する要素を構成する方法を与える(自然演繹の導入則に対応)。

\begin{prooftree} \AXC{$\Gamma, x:A\vdash B:C$} \AXC{$\Gamma\vdash \Pi x{:}A.C:s$} \BIC{$\Gamma\vdash \lambda x{:}A. B : \Pi x{:}A.C$} \end{prooftree}

(App): Abs規則の要素に値を適用する方法を与える(自然演繹の除去則に対応)。

\begin{prooftree} \AXC{$\Gamma\vdash A:\Pi x{:}B.C$} \AXC{$\Gamma\vdash A':B$} \BIC{$\Gamma\vdash A A' : C[x:=A']$} \end{prooftree}

(Wk): 文脈を水増しする(弱化)。

\begin{prooftree} \AXC{$\Gamma\vdash A:B$} \AXC{$\Gamma\vdash C:s$} \RightLabel{$~\small(x\notin\mathrm{dom}(\Gamma))$} \BIC{$\Gamma,x:C\vdash A:B$} \end{prooftree}

(Conv): β同値な対象の間で変換を行う。

\begin{prooftree} \AXC{$\Gamma\vdash A:B$} \AXC{$\Gamma\vdash B':s$} \RightLabel{$~\small (B=_\beta B')$} \BIC{$\Gamma\vdash A:B'$} \end{prooftree}

判断 $$J$$ の 導出(derivation) を、「判断の有限列 $J_1,\ldots,J_n=J$ であって、各 $1\leq i\leq n$ に対して結論が $$J_i$$ で前提が $\qty{J_j\mid j<i}$ に含まれるような推論規則が存在するもの」とする。

判断 $\Gamma\vdash M:A$ の導出が存在するとき、 $\Gamma\vdash M:A$ が 導出可能である(derivable) という。このことを単に $\Gamma\vdash M:A$ と書くことがある。

最後に純粋型システムを1つ定義し、導出の例を示す。導出は通常の証明論のように木構造で書くこととする。

例.

次のように純粋型システムを定義する。これは後述のλキューブにおける $\boldsymbol{\lambda 2}$ (system F)と等価である。

$\sorts=\qty{\Type,\Kind}$
$\axioms=\qty{\tuple{\Type,\Kind}}$
$\rules=\qty{(\Type,\Type),(\Kind,\Type)}$

このもとで、 $\vdash \Pi P{:}\Type.P\to P:\Type$ を示す(なお、これは冒頭の説明の多相関数 id の型が実際に型であることを表している)。

まず、 $P:\Type\vdash P\to P:\Type$ を示す( $P\to P$ は $\Pi x{:}P.P$ の略記であることに注意)。

\begin{prooftree} \AXC{}\LeftLabel{$\small\text{(Ax)}$}\UIC{$\vdash\Type:\Kind$} \LeftLabel{$\small\text{(Var)}$} \UIC{$P:\Type\vdash P:\Type$} \AXC{}\LeftLabel{$\small\text{(Ax)}$}\UIC{$\vdash\Type:\Kind$} \LeftLabel{$\small\text{(Var)}$} \UIC{$P:\Type\vdash P:\Type$} \AXC{}\LeftLabel{$\small\text{(Ax)}$}\UIC{$\vdash\Type:\Kind$} \LeftLabel{$\small\text{(Var)}$} \UIC{$P:\Type\vdash P:\Type$} \LeftLabel{$\small\text{(Wk)}$} \BIC{$P:\Type, x:P \vdash x:P$} \LeftLabel{$\small\text{(Prod)}$} \BIC{$P:\Type \vdash P \to P : \Type$} \end{prooftree}

最後のステップで規則 $(\Type,\Type)$ が使われている。次に、この導出図を $\D$ として、全体の導出図を以下のように構成できる。

\begin{prooftree} \AXC{}\LeftLabel{$\small\text{(Ax)}$}\UIC{$\vdash\Type:\Kind$} \AXC{$\D$}\noLine\UIC{$P:\Type\vdash P\to P:\Type$} \LeftLabel{$\small\text{(Prod)}$} \BIC{$\vdash \Pi P{:}\Type. P\to P:\Type$} \end{prooftree}

最後のステップで規則 $(\Kind,\Type)$ が使われている。

λキューブ

λキューブとは、PTSの特別な場合として特徴づけられる8つの型システムのことである。以下では $\sorts=\qty{\ast,\Box},~\axioms = \qty{\tuple{\ast,\Box}}$ とする。 $\sorts$ の要素はそれぞれ以下を表す。

$\ast$ : (真の)型の集まり
$\Box$ : カインドの集まり

$\rules$ としてあり得る要素は( $$s_2=s_3$$ として)4通りあり、それぞれ冒頭の説明の4つの場合に対応する。

$(\ast,\ast)$ : 項の中の項を抽象化(通常の関数)
$(\Box,\ast)$ : 項の中の型を抽象化(多相関数)
$(\ast,\Box)$ : 型の中の項を抽象化(依存型)
$(\Box,\Box)$ : 型の中の型を抽象化(型構成子)

$\rules$ の要素の組み合わせを色々と変えることで、以下8つの体系を得る。表には対応する論理体系を載せてあるが、どれも直観主義論理であることに注意されたい。

体系の名前	$(\ast,\ast)$	$(\Box,\ast)$	$(\ast,\Box)$	$(\Box,\Box)$	等価な型システム	対応する論理体系
$\boldsymbol{\lambda_\to}$	〇	×	×	×	単純型付きλ計算	命題論理
$\boldsymbol{\lambda 2}$	〇	〇	×	×	system F	2階命題論理
$\boldsymbol{\lambda \textbf{P}}$	〇	×	〇	×	Logical Framework (LF)	述語論理
$\boldsymbol{\lambda \underline{\omega}}$	〇	×	×	〇		弱高階命題論理
$\boldsymbol{\lambda\textbf{P}2}$	〇	〇	〇	×		2階述語論理
$\boldsymbol{\lambda\omega}$	〇	〇	×	〇	system Fω	高階命題論理
$\boldsymbol{\lambda\textbf{P}\underline{\omega}}$	〇	×	〇	〇		弱高階述語論理
$\boldsymbol{\lambda\textbf{C}}$	〇	〇	〇	〇	Calculus of Construction (CC)	高階述語論理

これらの型システム間の関係は、しばしば下図のような立方体で表される。これを λキューブ(lambda-cube) という。

\xymatrix@-1pc{ {}\\ {}\\ {}\\ {}\\ &{\scriptsize(\Box,~\Box)} \\ {} \ar[u]^{(\Box,~\ast)} \ar[ur] \ar[r]_{(\ast,~\Box)} & {} } \qquad \xymatrix@!=10pt{ & {\boldsymbol{\lambda\omega}} \ar@{-}[rr]\ar@{-}'[d][dd] & & {\boldsymbol{\lambda\textbf{C}}} \ar@{-}[dd] \\ {\boldsymbol{\lambda 2}} \ar@{-}[ur]\ar@{-}[rr]\ar@{-}[dd] & & {\boldsymbol{\lambda\textbf{P}2}} \ar@{-}[ur]\ar@{-}[dd] \\ & {\boldsymbol{\lambda \underline{\omega}}} \ar@{-}'[r][rr] & & {\boldsymbol{\lambda\textbf{P}\underline{\omega}}} \\ {\boldsymbol{\lambda_\to}} \ar@{-}[rr]\ar@{-}[ur] & & {\boldsymbol{\lambda \textbf{P}}} \ar@{-}[ur] }

λキューブに属する8つの型システムは、どれも以下のようなよい性質を満たす。

命題. λキューブの性質

割り当ての一意性: $\Gamma\vdash M:A$ かつ $\Gamma\vdash M:A'$ ならば $A=_\beta A'$
主部簡約定理: $\Gamma\vdash M:A$ かつ $M\reds M'$ ならば $\Gamma\vdash M':A$
強正規化性: $\Gamma\vdash M:A$ ならば、 $$M$$ の任意の簡約列の長さは有限
Church-Rosser性: $M\reds M',~M\reds M''$ ならば、ある $N\in\Lambda$ が存在して $M'\reds N,M''\reds N$
判断 $\Gamma\vdash M:A$ が導出可能か否かは決定可能である

参考文献

Luo, Z. (1994). Computation and reasoning. Oxford University Press.
Pierce, B. C. (2013). 『型システム入門プログラミング言語と型の理論』. オーム社.
Sørensen, M. H., & Urzyczyn, P. (2006). Lectures on the Curry-Howard isomorphism. Elsevier.
Wadler, P., Wen K., and Siek, J. G. (2022). Programming Language Foundations in Agda (version 22.08).
龍田真. (1992). 『レクチャーノート／ソフトウェア工学1 型理論』. 近代科学社.

例に使うのはAgda風の擬似コードである(だいたいHaskellみたいなものだと思っていただければよい)。 ↩
ここでは多相型には明示的には型を渡す必要があり、このような定義をexplicit polymorphismという。一方で、OCamlのような言語で採用されている多相型では型を引数として渡す必要はなく、引数の項の型から自動的に関数の型が決まる。このような定義をimplicit polymorphismという。 ↩
このカインドは、型システム・定理証明支援系によっては Set や Prop の名前で呼ばれることもある(この2つが別々に存在することもある)。体系によって性質(e.g. 可述性, proof-irrelevance)が異なるので注意が必要である。 ↩
Type 自体は型ではない。Type : Type を許容すると、集合論において全ての集合の集まりを集合だとしてしまった場合と同様に、パラドックスが生じる(矛盾に対応する型 ⊥ の項を構成できる)。 ↩
Type に属する型が、Π(A : Type). ... のように Type 全体への量化を含むということは、定義において自分自身が言及されているということであり、これは循環的であり奇妙さを感じるかもしれない。が、さしあたり問題はない。このような型の定義を 非可述的である(impredicative) といい、ある程度制限された形で導入する限りでは、非可述性を許容しても型システムは壊れない(矛盾を引き起こさない)ことが知られている。 ↩
定理証明支援系Coqではこれに相当する措置が取られている。Coqには、ここでの Type に相当するものが $\mathsf{Prop}$ , $\mathsf{SProp}$ , $\mathsf{Set}$ の計3つある。これらは全て $\mathsf{Type}_0$ という1つ上のレベルのソートに属する。詳しくはCoqのレファレンスなどを参照のこと。 ↩
「追加の条件」の部分には、形式体系の内部で妥当性が扱われるような言明(ここでは判断 $\Gamma\vdash M:A$ )ではなく、体系の外部で判定が行われるような言明が入る。これらが線の上側に(前提と並べて)書かれることもあるが、混同を防ぐために当サイトではそのような書き方は避ける。 ↩